
はじめに
先日公開された3次元姿勢推定の手法であるEpipolar Transformersを紹介します。Human3.6Mという3次元姿勢推定で一般的なベンチマークとして使われるデータセットにおいて、最高精度を達成しています。また、Hand Pose Estimation (手の骨格の推定)でも既存の手法の精度を超えています。
以下が今回紹介するEpipolar Transformersの論文です。
https://arxiv.org/abs/2005.04551
実装も公開されています。(記事執筆時点で100starを超えていて注目されていることが分かります)
arXivでの公開は2020/05/10で、来月のCVPR2020に採録されています。 また、CVPR 2020 Workshop On Towards Human-Centric Image/Video Synthesis, and the 4th Look Into Person (LIP) Challenge のワークショップのbest paperにも選ばれています。
画像入力の3次元姿勢推定には大きく、single-viewとmulti-viewの2つがあります。single-viewは1枚の画像を入力にして3次元姿勢を推論するもので、multi-viewは複数視点の複数枚の画像を入力にして3次元姿勢を推論するものです。
single-viewは1枚の入力でよいのでカメラのキャリブレーションもいらず、手軽に推論を行うメリットがある一方で、深度情報を取ることが難しく、推論の精度は落ちてしまいます。multi-viewは環境のセッティングは面倒なもののより高い精度での推論を行うことができるメリットがあります。今回の手法は後者のmulti-viewに対応する手法です。
個人的にはsingle-viewのほうがシンプルで好きですが、single-viewはどうしても予測に曖昧さは残りますし、ある程度精度を上げようと思うと、multi-viewは必要なので、取っ掛かりとして読んでみようかなと思いました。
提案手法の特徴
multi-viewの3次元姿勢推定としてよく行われる方法は、以下の2ステップです。
- 各視点において2次元姿勢推定を行う。
- 得られた2次元姿勢推定の結果とカメラパラメータに基づいて三角測量 (triangulation)を行い、3次元的位置を推定する。
三角測量は、カメラの3次元的位置とそのカメラから対象の点の角度から、対象の点の3次元的位置を推定することを指します。
この機構で課題となるのは、各2次元姿勢推定のモデルは3次元的情報を使っていないことです。以下の図のように三角測量 (triangulation)の部分ではじめて3次元的情報を使うことになってしまいます。このため、例えばオクルージョンの影響などで、1ステップ目の姿勢推定で不正確な予測や欠損が起きた場合、結果が悪くなってしまいます。

Epipolar Transformersでは、2次元姿勢推定のモデルの中間レイヤーに相互の情報を補完するためのモジュールを導入して、この問題を改善することを目的にしています。そして、このモジュールのキモにエピポーラ幾何を使っています。
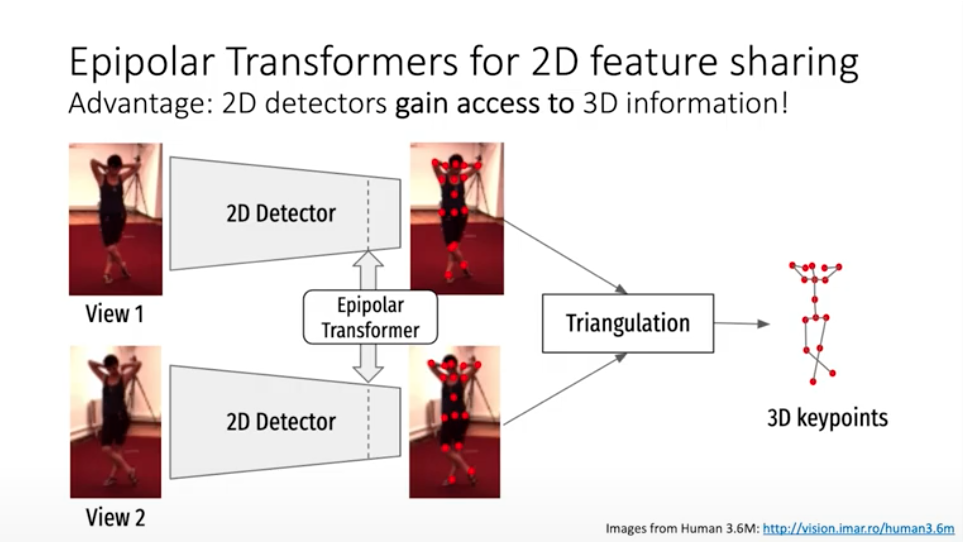
このモジュールは軽量で簡単に適用できるという点は魅力的です。また、エピポーラ幾何を使うコア部分はうまさを感じます。納得感があり、結果も出ているので、面白い手法だなあと思いました。
以下の著者のYoutubeでの説明が分かりやすかったので、上記説明はこちらも参照しています。短い動画なのでこちらも御覧ください。
提案手法の詳細
Epipolar Transformersのモジュールについて説明します。概要は以下の図のような形式です。Reference viewとSource viewのそれぞれが各視点からの画像で、特徴量として、HxWx256というサイズのレイヤーをそれぞれ使っています。fused featuresの部分がモジュールとしての出力になりますが、このサイズもHxWx256です。このサイズが同じであるため、中間レイヤーを取ってきて、それを変換してそのまま返すだけで実装できるため、既存のモデルに適用しやすい構造になっています。
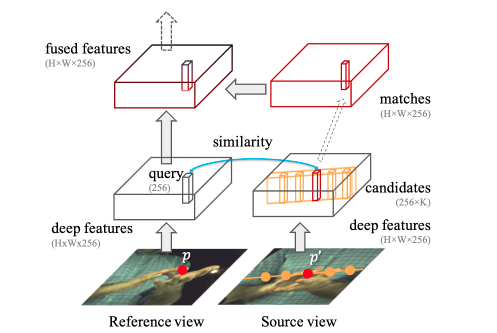
Epipolar Sampler
論文の肝であるEpipolar Samplerについて説明します。
まず、エピポーラ(Epipolar)幾何について簡単に説明します。以下の図の点Cが2つのカメラを表しています。そして、2つの面はカメラの投影面を表しています。各カメラからある点Pを見たときに、各面に投影される点がYです。各カメラ同士を結んだ線と投影面の交点をエピポーラ点といい、この点とYを含む直線をエピポーラ線といいます (図中のl)。カメラの位置関係が既知で、左のカメラで点Pを補足した場合、右のカメラで補足する点Pの位置はエピポーラ線上にのります。この関係をエピポーラ制約といいます。
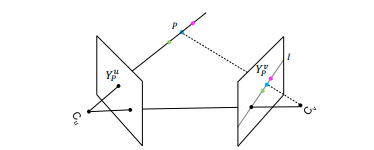
(図参照: https://arxiv.org/pdf/1909.01203.pdf)
エピポーラ幾何はこちらの記事が分かりやすかったです。3次元姿勢推定でちょくちょくエピポーラ幾何は出てきますね。 zellij.hatenablog.com
さて、話を戻しましょう。先程の図の特に以下の部分にまず注目します。まず、Reference側のある点のqueryに対応するSource側の画像のエピポーラ線がオレンジの部分です。
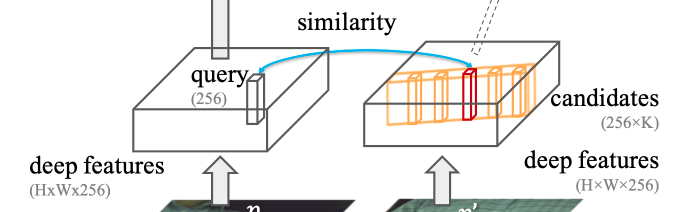
あるqueryに対するSource側の特徴量がエピポーラ線上にくることを仮定してこの部分から該当の点を抽出します。K個(論文中では64個)をサンプルして、queryとのcosine similarityで重み付けされた和を取って特徴量とします。
Feature Fusion Module
お見せしたモジュールの構成図のうち、Epipolar sampleは一部でした。最初にお見せしたものの構造は以下の図の(b)にあたります。実験として、(a)のような構成のモジュールも試してありましたが、(a)よりも(b)のほうが僅かに結果がよかったということで(b)が採用されています。
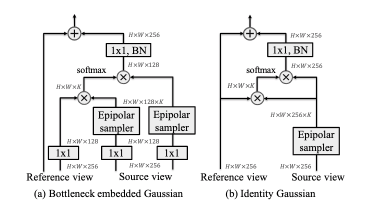
Epipolar samplerの出力を使って、softmaxにかけている部分はattentionのような構造になっていますが、これを著者はepipolar attentionと呼んでいます。これによって、エピポーラ線に沿った特徴量を使った重み付けが可能となります。
結果
結果は既存手法を上回る結果出ています。詳細が気になる方は論文を参照して下さい。基本的に、以下の2つの手法と比較しています。
- Cross View Fusion for 3D Human Pose Estimation [Qiu+ ICCV'19]
- Learnable Triangulation of Human Pose [Iskakov+ ICCV'19]
https://arxiv.org/abs/1909.01203arxiv.org
https://arxiv.org/abs/1905.05754arxiv.org
提案手法は、パラメータも少なく学習も比較手法に対して容易であるということですが、カメラのキャリブレーションは正確に行う必要があるということは要注意です。エピポーラ幾何を使っているので、カメラの位置関係が間違っていると前提が崩れてしまうためですね。
3D Pose Estimation参考資料
3D Pose Estimationに興味が出た方には以下がおすすめです。
終わりに
以上で、Epipolar Transformersの説明を終わります。エピポーラ幾何をうまく取り込んだモジュールを提案している部分のアイデアが光っていてかっこいい論文だと思いました。3次元姿勢推定でも可能であればsingle-viewでやりたいところですが、やはりmulti-viewのほうが精度は出そうであるし、実用的には使い分けをきっちりしていくことは大事だと思いました。